Contents
- 红黑树
- 1.红黑树的定义
- 2.红黑树操作简单例子
- 3.红黑树代码实现
- 3.1 红黑树插入操作
- 插入修复情形1:之前是棵空树,新插入的节点是树根。根据性质2,根节点必须是黑色。
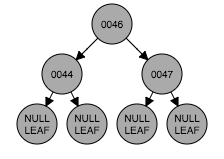
- 插入修复情形2:插入的节点的父节点是黑色的,这种情况下直接插入红色节点。(如图:插入节点46)
- 插入修复情形3: 插入的节点父节点以及叔父节点都是红色。
- 插入修复情形4:节点是父节点的右孩子(如图4.3中节点47),其父节点(44)是其祖父节点(50)的左孩子,其叔父节点是黑色(节点60)。
- 插入修复情形5:节点是父节点的左孩子,父节点是祖父节点的左孩子,叔父节点是黑色。
- 3.2 红黑树删除操作
- 删除修复情形1:节点是新的根。
- 删除修复情形2:如图2.1,兄弟节点(S)是红色。如图2.1
- 删除修复情形3:如图3.1,节点(N)、父节点(P)、兄弟节点(S)都是黑色。
- 删除修复情形4:节点和兄弟节点都是黑色,父节点是红色。
- 删除修复情形5:节点的兄弟节点是黑色,兄弟节点的左孩子是红色,右孩子是黑色。
- 删除修复情形6:节点是父节点的左孩子,其兄弟节点(图6.1中S节点)是黑色,并且兄弟节点的右孩子是红色节点。
- 4.红黑树Java实现完整代码
- 5.红黑树具体应用
- 6.参考
红黑树
1.红黑树的定义
红黑树是平衡二叉查找树(Balance Search Tree)的一种,它拥有良好的最坏运行时间,可以保证查找、删除、添加节点操作在O(log n)时间内,其中n表示节点数。
红黑树每个节点都带有颜色属性,红色或者黑色,除了BST的性质以外,还有以下性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面是一棵红黑树的例子,例子中为中序遍历降序排列,后面的操作中也按照这个顺序。
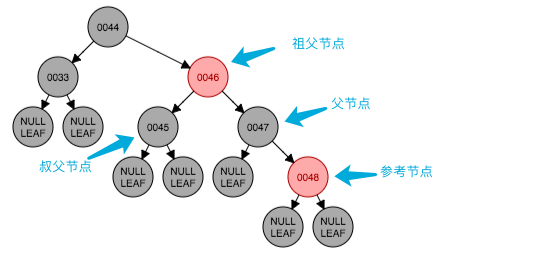
例子中以节点48作为参考节点,类比人类社会,将47节点叫做它的父节点,46叫做它的祖父节点,45叫做它的叔父节点。
2.红黑树操作简单例子
step 1 插入节点(44)
因为第一个节点是根节点,根据性质2,节点为黑色。
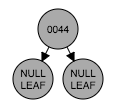
step 2 插入节点(45)
由于45大于44,所以作为节点44的右边孩子接入并设置为红色。可以看到性质5得到了保持。
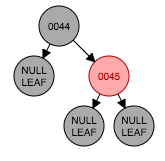
step 3 插入节点(46)
46大于节点45应该作为右孩子接入设置为红色。显然违反了性质4
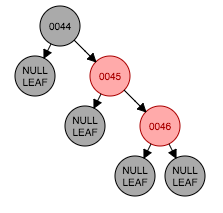
以节点45为轴做左旋转,违反了性质2、4、5。
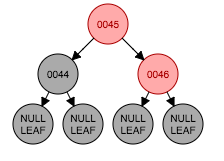
将45改为黑色(符合了性质2、4),将节点44改为红色(符合性质5)??事实上我也可以将46节点涂成黑色??得到全黑色节点
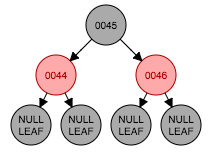
step 4 插入节点(47)
47大于节点46作为右孩子接入设置为红色。违反了性质4。
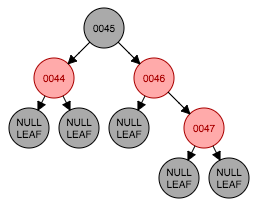
这个时候47的父节点46与叔父节点都是红色 ,则祖父节点45颜色下降。但仍然违反性质2,因为47的祖父节点45是根节点。
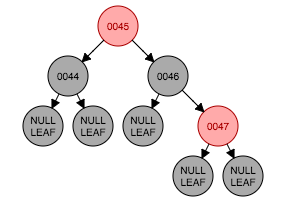
将45颜色变为黑色。
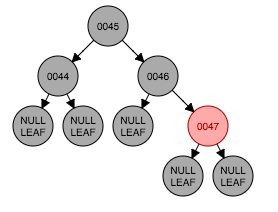
step5 删除节点(45)
要删除节点45,首先将其左子树中最大节点44。
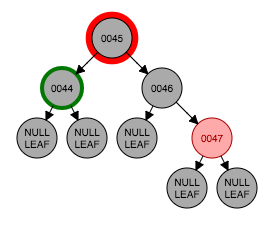
将44节点的值拷贝到45节点处,移除老的44节点。此时违反了性质5。
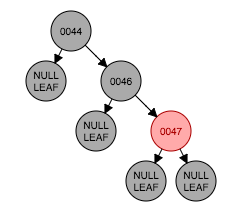
以46节点为轴进行坐旋转。但仍然违反性质5。
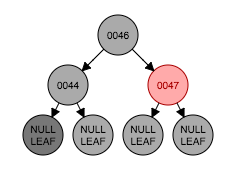
将47节点设置为黑色。
3.红黑树代码实现
上面简单例子中插入以及删除节点操作并没有完全涵盖所有的情况。下面来看一看红黑树java代码实现。根据具体每一类情况,形成与之对应的代码操作。下面情况对应的配图都在对应情况的下方,比如有两个图3.1,分别对应前面小标题。
3.1 红黑树插入操作
红黑树是BST(Binary Search Tree,二叉查找树),除了需要执行BST的插入操作以外还要根据红黑树的性质进行调整,因为直接插入节点有可能会破坏红黑树的结构。红黑树插入节点都按照红色插入。(维基百科解释:如果设为黑色,就会导致根到叶子的路径上有一条路上,多一个额外的黑节点,这个是很难调整的。但是设为红色节点后,可能会导致出现两个连续红色节点的冲突,那么可以通过颜色调换和树旋转来调整。) 。关于插入后的恢复情形有下面5种。
插入修复情形1:之前是棵空树,新插入的节点是树根。根据性质2,根节点必须是黑色。
</font>
 (图1)
(图1)
private void insertFixUpCase1(Node node) {
if (node.parent == null) {
//情形1:如果插入节点是根节点,则设置为黑色
root = node;
node.color = Color.BLACK;
} else {
insertFixUpCase2(node);
}
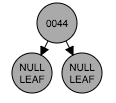
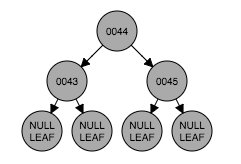
}插入修复情形2:插入的节点的父节点是黑色的,这种情况下直接插入红色节点。(如图:插入节点46)
</font>
 (图2.1)
(图2.1)
 (图2.2)
(图2.2)
private void insertFixUpCase2(Node node) {
if (node.parent.color == Color.BLACK) {
//父节点是黑色
//情形2:如果父节点是黑色的,所有性质都没有受到影响
//不需要做什么
} else {
insertFixUpCase3(node);
}
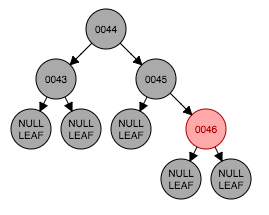
} 插入修复情形3: 插入的节点父节点以及叔父节点都是红色。
从图3.1为插入前状态,插入节点42后成为节点43的左孩子,这时性质4遭到破坏,因为存在连续红色节点(图3.2)。要满足性质4需要将祖父节点(44)与父节点、叔父节点的颜色进行交换,如图3.3。性质2此时无法满足因为根节点44是红色。其实给出图片的例子中44是一个根节点,很多情况中44并不是根节点。此时将44按照新插入的节点从情形1开始处理,那么应该涂成黑色,如图3.4
</font>
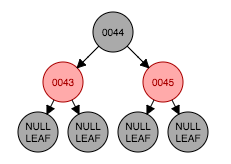 (图3.1)
(图3.1)
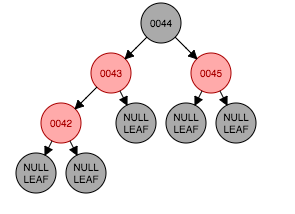 (图3.2)
(图3.2)
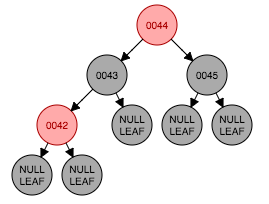 (图3.3)
(图3.3)
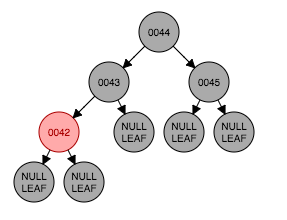 (图3.4)
(图3.4)
private void insertFixUpCase3(Node node) {
//父节点是红色
Node uncleNode = getUncleNode(node);
if (uncleNode != null && uncleNode.color == Color.RED) {
//叔父节点是红色
//情形3:父节点和叔父节点都是红色。这种情况下,我们需要将祖父节点的颜色下沉一层,即祖父节点变成红色,父节点和叔父变成黑色。
uncleNode.color = Color.BLACK;
node.parent.color = Color.BLACK;
getGrandparentNode(node).color = Color.RED;
//调整
insertFixUpCase1(getGrandparentNode(node));
} else {
//叔父节点是黑色
//情形4:父节点是红色,叔父节点是黑色,祖父节点肯定是黑色的,要不然就违反了红黑树不能连续红色节点的性质
insertFixUpCase4(node);
}
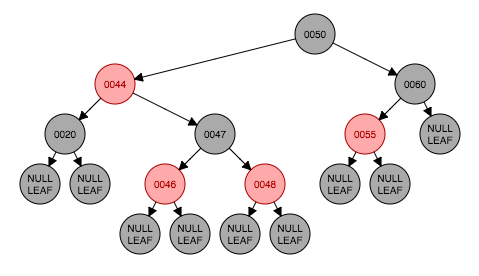
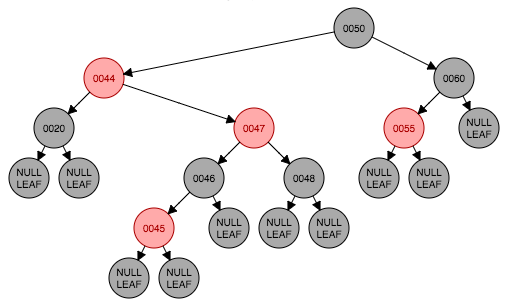
}插入修复情形4:节点是父节点的右孩子(如图4.3中节点47),其父节点(44)是其祖父节点(50)的左孩子,其叔父节点是黑色(节点60)。
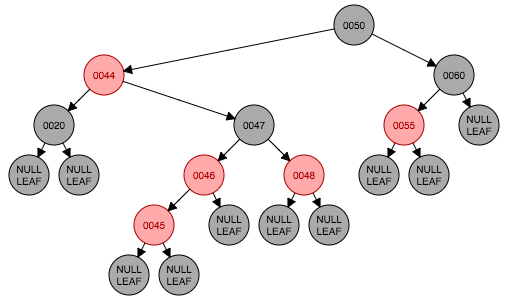
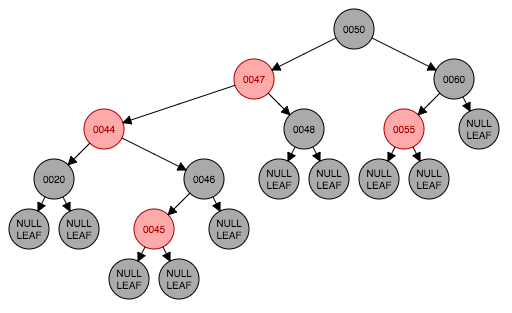
这种情况的对称情况也属于同一情况。下面来看一下这种情形是怎么出现的,图4.1是初始状态,插入节点45,红色,图4.1到4.3这个过程实际上是情形3的处理过程。从4.3到4.4才是情形4的场景,这种情况下以新插入节点(这里是47)作为旋转轴做一次左旋转,对称的情况做右旋转。此时红黑树的性质5仍然没有满足,下面交给情形5处理。
</font>
 (图4.1)
(图4.1)
 (图4.2)
(图4.2)
 (图4.3)
(图4.3)
 (图4.4)
(图4.4)
private void insertFixUpCase4(Node node) {
if (node.parent.leftChild == node && getGrandparentNode(node).rightChild == node.parent) {
rotateRight(node);
} else if (node.parent.rightChild == node && getGrandparentNode(node).leftChild == node.parent) {
rotateLeft(node);
}
insertFixUpCase5(node);
}插入修复情形5:节点是父节点的左孩子,父节点是祖父节点的左孩子,叔父节点是黑色。
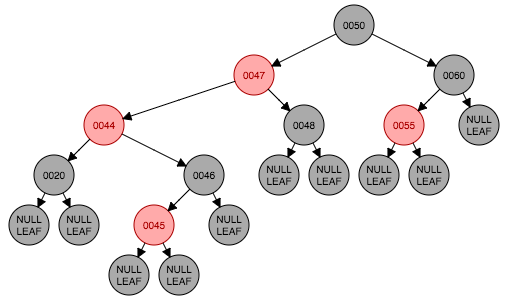
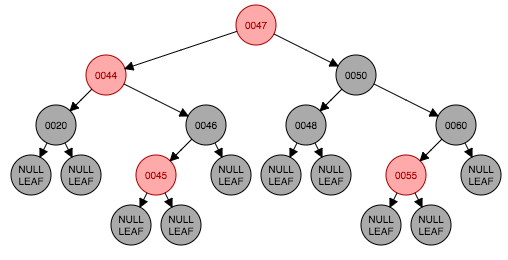
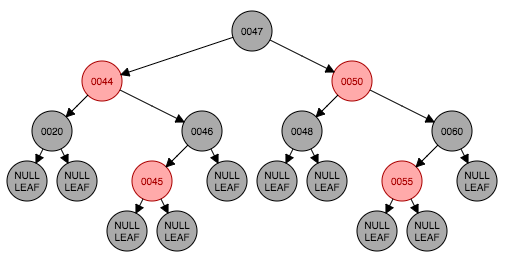
我们直接看图5.1(实际上和图4.4是一张图,想知道来龙去脉可以看这里)。此时性质5被破坏,我们先以节点47为轴做右旋转得到图5.2,再将原先父节点(节点47)与原先祖父节点(节点50)颜色进行交换,完成,如图5.3。
</font>
 (图5.1)
(图5.1)
 (图5.2)
(图5.2)
 (图5.3)
(图5.3)
private void insertFixUpCase5(Node node) {
node.parent.color = Color.BLACK;
getGrandparentNode(node).color = Color.RED;
if (node == node.parent.leftChild && node.parent == getGrandparentNode(node).leftChild) {
rotateRight(node.parent);
} else {
rotateLeft(node.parent);
}
}3.2 红黑树删除操作
同样删除操作除了需要执行BST的删除操作以外还要根据红黑树的性质进行调整。关于删除后的恢复情形有下面6种。
删除修复情形1:节点是新的根。
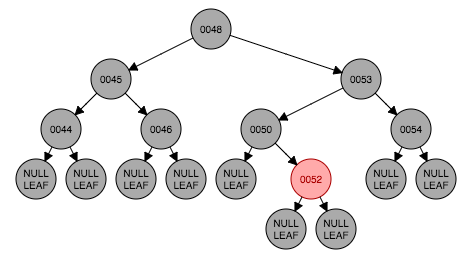
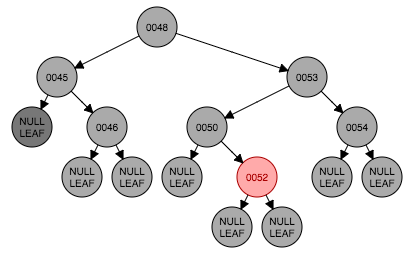
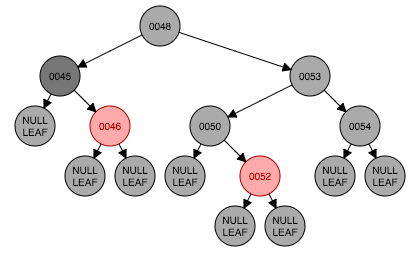
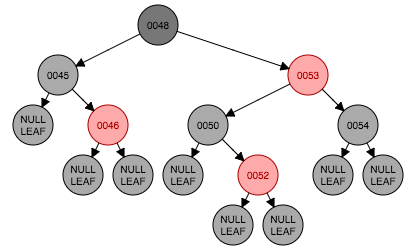
图1.1是删除前的初始状态,要删除节点44,找到节点44对它进行删除,从节点44左孩子中寻找最大那个节点(这里左孩子是叶子节点)将内容替换到原节点44。因为删除的节点是黑色节点所以性质5被破坏。在情形1之前,这里先遇到了情形3(图1.2-1.3),节点46变换成红色节点,紧接着还是情形3,节点53也要改成红色节点(图1.3-1.4)。情形1出现了。。。节点48是根节点,且是黑色,什么都不需要做。
</font>
 (图1.1)
(图1.1)
 (图1.2)
(图1.2)
 (图1.3)
(图1.3)
 (图1.4)
(图1.4)
private void deleteFixUpCase1(Node node) {
if (node.parent == null) {
//情形1:node是新的根
} else {
deleteFixUpCase2(node);
}
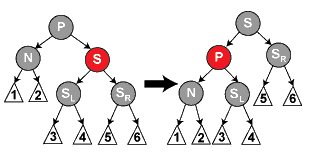
}删除修复情形2:如图2.1,兄弟节点(S)是红色。如图2.1
这种情况下以兄弟节点S为转轴做一次左旋转,并将原父节点(P)与原兄弟节点(S)颜色做一下交换。在真实中的例子情参看情形4的例子。
</font>
 (图2.1)
(图2.1)
private void deleteFixUpCase2(Node node) {
Node sib = sibling(node);
if (sib.color == Color.RED) {
sib.color = Color.BLACK;
node.parent.color = Color.RED;
if (node == node.parent.leftChild) {
rotateLeft(sib);
} else {
rotateRight(sib);
}
}
deleteFixUpCase3(node);
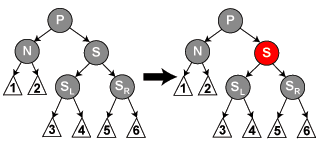
}删除修复情形3:如图3.1,节点(N)、父节点(P)、兄弟节点(S)都是黑色。
这时我们将兄弟节点颜色设置为红色。
</font>
 (图3.1)
(图3.1)
private void deleteFixUpCase3(Node node) {
Node sib = sibling(node);
if (sib != null
&& sib.leftChild != null
&& sib.rightChild != null
&& node.parent.color == Color.BLACK
&& sib.color == Color.BLACK
&& sib.leftChild.color == Color.BLACK
&& sib.rightChild.color == Color.BLACK) {
sib.color = Color.RED;
deleteFixUpCase1(node.parent);
} else {
deleteFixUpCase4(node);
}
}删除修复情形4:节点和兄弟节点都是黑色,父节点是红色。
这种情况下,我们将父节点和兄弟节点的颜色进行交换。
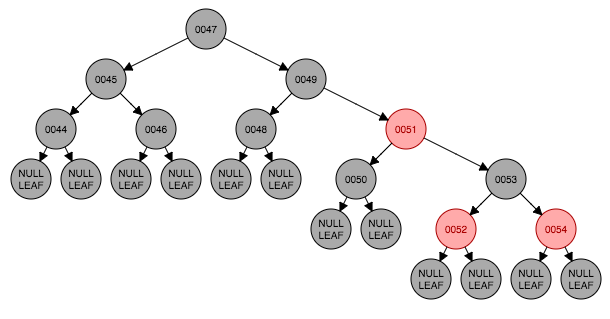
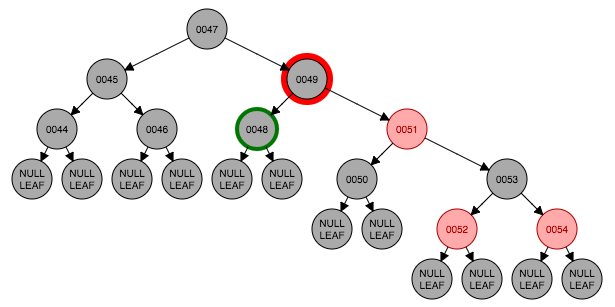
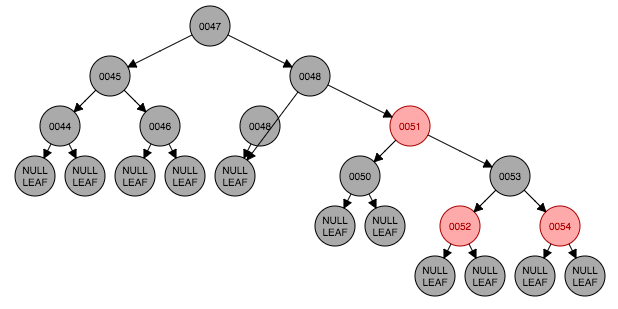
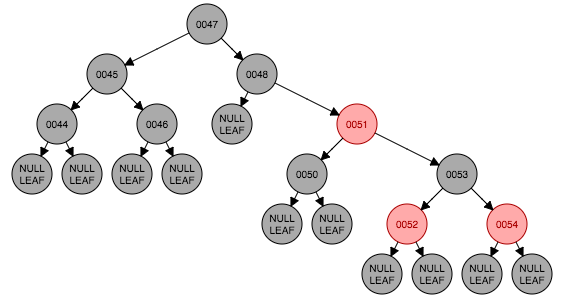
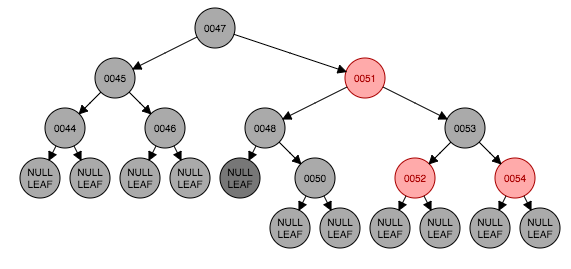
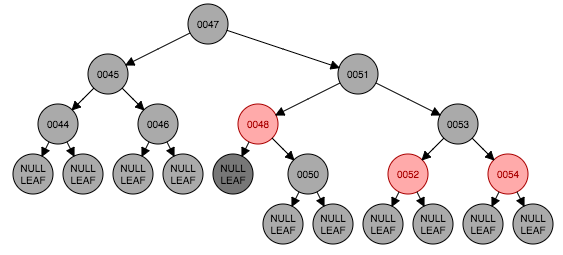
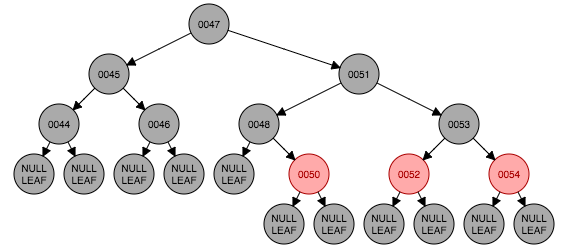
下面演示一个例子。例子开始状态如图4.1,要删除节点49,从左侧树中选出最大的节点48的值替换到49节点,这时候如图4.4。以48节点的左子树为基准,符合情形2,以51为转轴做一次左旋转,并交换父节点(48)与兄弟节点(51)的颜色结果如图4.6。这时符合情形4,将父节点48与兄弟节点50交换颜色,转换结束如图4.7。
</font>
 (图4.1)
(图4.1)
 (图4.2)
(图4.2)
 (图4.3)
(图4.3)
 (图4.4)
(图4.4)
 (图4.5)
(图4.5)
 (图4.6)
(图4.6)
 (图4.7)
(图4.7)
删除修复情形5:节点的兄弟节点是黑色,兄弟节点的左孩子是红色,右孩子是黑色。
如图5.1,图中只是兄弟节点部分。S即为兄弟节点。这时以兄弟节点的左孩子进行右旋转。节点对称的情况,旋转操作也是对称的。关于树旋转,我参考的是维基百科Tree Ratation中的旋转方式。情况5在真实操作中的情况可以参考情况6给出的图解。
</font>
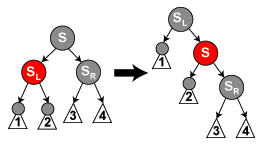 (图5.1)
(图5.1)
private void deleteFixUpCase5(Node node) {
Node sib = sibling(node);
if (sib.color == Color.BLACK) {
if (node == node.parent.leftChild
&& sib.rightChild.color == Color.BLACK
&& sib.leftChild.color == Color.RED
) {
sib.color = Color.RED;
sib.leftChild.color = Color.BLACK;
rotateRight(sib.leftChild);
} else if (node == node.parent.rightChild
&& sib.leftChild.color == Color.BLACK
&& sib.rightChild.color == Color.RED) {
sib.color = Color.RED;
sib.rightChild.color = Color.BLACK;
rotateLeft(sib.rightChild);
}
}
deleteFixUpCase6(node);
}删除修复情形6:节点是父节点的左孩子,其兄弟节点(图6.1中S节点)是黑色,并且兄弟节点的右孩子是红色节点。
这种情况下我们首先交换父节点和兄弟节点的颜色,并且将兄弟节点的右孩子颜色设置为黑色。然后以兄弟节点为旋转轴做左旋转。
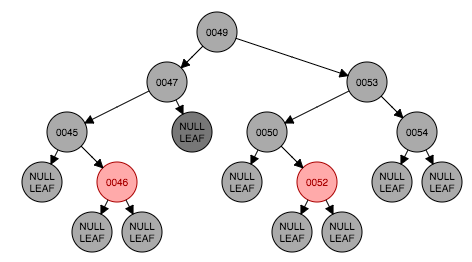
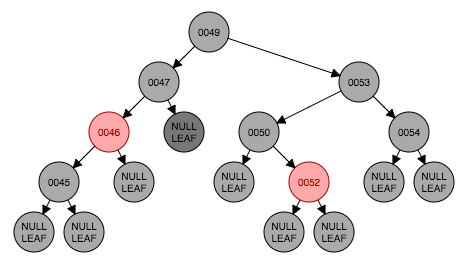
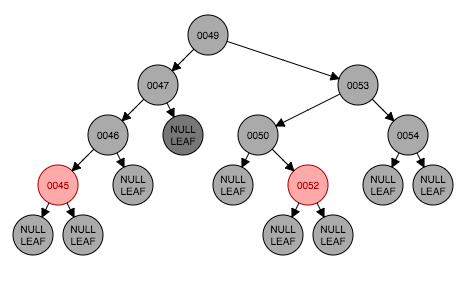
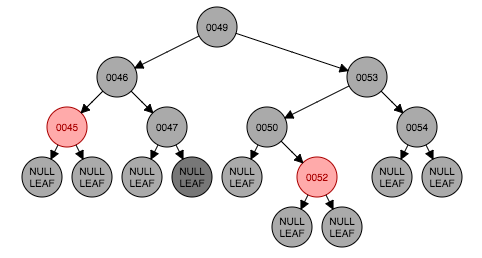
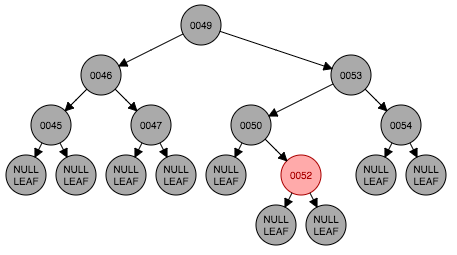
从图6.2开始做一个包含情况6的真实情况的例子。删除节点48如图6.3,原48处被叶子节点取代。这时满足情形5,处理后得到图6.5。情形6出现了,以节点46为转轴做一次右旋转,并且将节点46的左孩子设置为黑色。转换结束。
</font>
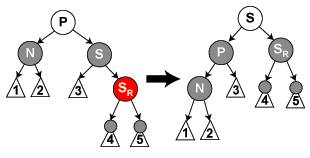 (图6.1)
(图6.1)
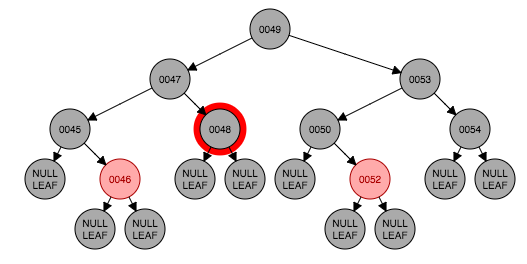 (图6.2)
(图6.2)
 (图6.3)
(图6.3)
 (图6.4)
(图6.4)
 (图6.5)
(图6.5)
 (图6.6)
(图6.6)
 (图6.7)
(图6.7)
private void deleteFixUpCase6(Node node) {
Node sib = sibling(node);
sib.color = node.parent.color;
node.parent.color = Color.BLACK;
if (node == node.parent.leftChild) {
sib.rightChild.color = Color.BLACK;
rotateLeft(sib);
} else {
sib.leftChild.color = Color.BLACK;
rotateRight(sib);
}
}4.红黑树Java实现完整代码
https://github.com/mingbozhang/blogcode/tree/master/algorithms/src/main/java/com/bob/datastructure/rbtree
5.红黑树具体应用
Java中的TreeMap
6.参考
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/03.01.md
https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91
https://zh.wikipedia.org/wiki/%E6%A0%91%E6%97%8B%E8%BD%AC
https://en.wikipedia.org/wiki/Tree_rotation